In this article we’ll give a brief introduction into what a low pass filter is, why we need it and how it works. Function of the interest you have you can jump to the desired section detailed below:
- Introduction to signals and filters
- Low pass filter circuit (RC)
- Low pass filter parameters
- Low pass filter mathematical analysis
- Low pass filter simulation
- Low pass filter calculator
Introduction to signals and filters
In engineering, whether it’s electrical, mechanical, civil or other, we often have to deal with signals. Some of those signals, for example, are coming from measurement sensors. You might have to measure pressure, speed, temperature and most of these measurements will be translated into electronic signals (e.g. voltage).
Here is where a filter comes into play. All of the signals coming from sensors have “noise” into them. Any measured signal is made up from several “sub-signals” or components, each with their own frequency and amplitude. The noise of a signal has higher frequency than the desired (ideal) signal being measured (e.g. speed of a shaft).
Image: Measured signal – ideal signal plus noise
As example let’s assume that we have a “measured” signal coming from a sensing device (sensor). We can regard the “measured” signal as an “ideal” signal which has been altered by some noise. The role of the low pass filter is to remove the noise and output a signal as close as possible to the “ideal” signal. The “measured” signal is the sensor input and the filtered signal is the sensor output. The filtered (output) signal will never be exactly as the “ideal” signal because the filtering process will induce some phase shift and attenuation onto it.
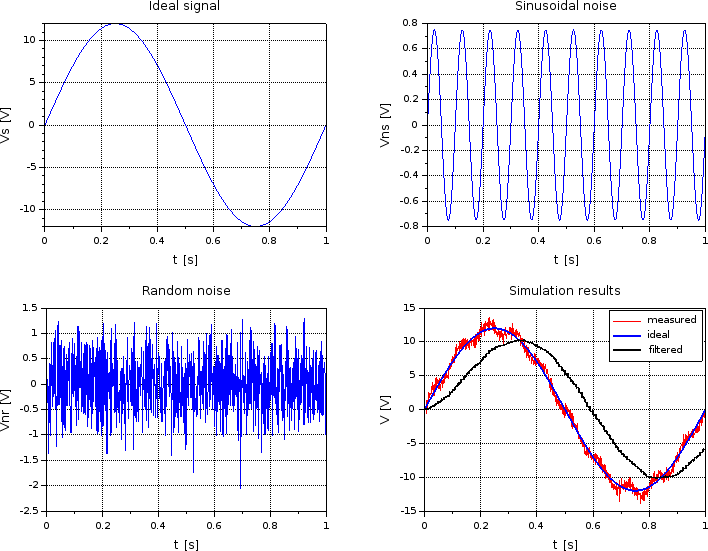
As you can see in the image below, the filtered signal (blue) has the amplitude a bit smaller than the measured signal and it’s also a bit delayed (shifted to the right). For this reason the parameters of the low pass filter must be tuned in such a way so that the output signal is smooth enough and in the same time its amplitude and phase (delay) are not too much impacted.
Image: Low pass filter example signal
A low pass filter is called “low pass” because it lets only the low frequency components of a signal to pass through and blocks the high frequency components (like noise).
A low pass filter has a specific cut-off frequency, which decides which frequencies are passing and which are being blocked (filtered). If a component of a signal has a frequency lower than the cut-off frequency, then it will pass, otherwise it will be blocked (filtered, cut off).
The cut-off frequency is also called breakpoint or corner frequency.
A low pass filter allows the engineer to make use of the desired signal to be measured (speed, pressure, temperature) by removing the unnecessary components of the signal (noise). This separation of noise from actual signal is really important because otherwise the measured signal will contain values which are not present in reality.
The noise usually occurs as a component of a measured signal due to environment conditions, where the measurement is being done and the actual construction of the measuring device (sensor, power supply, sensing element, etc.).
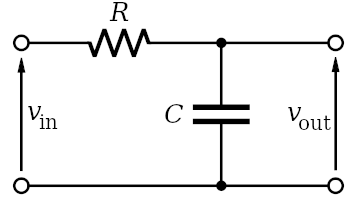
Low pass filter circuit (RC)
A simple implementation of a low pass filter is the RC circuit. The Resistor Capacitor (RC) circuit contains an input voltage vIN [V] and a resistor (R) connected in series with a capacitor (C). The filtered output voltage vOUT [V] is measured across the capacitor.
Image: Low pass filter – RC circuit
In a measurement setup we can imagine that the input voltage is coming from the sensor and the output voltage is the filtered signal.
A detailed mathematical description, modeling and simulation of the RC circuit can be found in the article Mathematical models and simulation of electrical systems.
For a better understanding of how the low pass filter works, we are going to do some simulations. For this we are going to derive the mathematical model of the low pass filter (RC circuit) and use it in dedicated simulation environments like Scilab/Xcos.
Applying Kirchhoff’s Laws we can derive the differential equation of the RC circuit as [1]:
\[v_{IN}(t) = v_{OUT}(t) + RC \cdot \frac{dv_{OUT}}{dt} \tag{1} \]From (1) we can write the expression of the output voltage (filtered) as:
\[v_{OUT}(t) = v_{IN}(t) – RC \cdot \frac{dv_{OUT}}{dt} \tag{2} \]This equation can be solved assuming a step input Vi of the input voltage [2]. In this case we obtain the expression in time of vOUT function of Vi, R and C.
\[v_{OUT}(t) = V_{i} \left ( 1 – e^{- \frac{1}{RC}t} \right ) \tag{3}\]Equation (3) defines the step response of the low pass filter, which shows the behaviour of the output signal of the filter (vOUT) when a step input signal (vIN) is applied to the filter.
Low pass filter parameters
There are several parameters defining a RC low pass filter. The main parameters are:
- cut-off angular frequency, ωc [rad/s]
- cut-off frequency, fc [Hz]
- period, T [s]
- time constant, τ [-]
When the low pass filter is applied to a periodic input signal of frequency f [Hz], we can also calculate these parameters of the low pass filter:
- phase shift, φ [rad]
- capacitive reactance, Xc [Ω]
- impedance, Z [Ω]
- amplitude of the output voltage, VOUT [V]
The cut-off angular frequency of the low pass filter is defined as:
\[ \omega_{c} = \frac{1}{RC} \text{ [rad/s]} \tag{4} \]The cut-off frequency of the low pass filter is calculated as:
\[ f_{c} = \frac{\omega_{c}}{2 \pi} = \frac{1}{2 \pi RC} \text{ [Hz]} \tag{5} \]The cut-off frequency “decides” which signals are allowed to pass. Signals with frequencies lower than the cut-off frequency are passing while the ones with higher frequency are blocked (filtered).
The period of the low pass filter is calculated as:
\[ T = \frac{1}{f_{c}} = \frac{2 \pi}{\omega_{c}} = 2 \pi RC \text{ [s]} \tag{6} \]The time constant of the low pass filter is calculated as:
\[ \tau = \frac{1}{\omega_{c}} = \frac{1}{2 \pi f_{c}} = RC \text{ [s]} \tag{7} \]The phase shift of the low pass filter is calculated as:
\[ \varphi = – \arctan \left ( 2 \pi f RC \right ) \text{ [rad]} = – \arctan \left ( 2 \pi f RC \right ) \frac{180}{\pi} [^{\circ}] \tag{8} \]The phase shift shows how much the output (filtered) signal is delayed compare with the input (measured signal). The higher the phase shift, the longer the delay.
The capacitive reactance of the low pass filter is calculated as:
\[ X_{C} = \frac{1}{2 \pi f C} \text{ [} \Omega \text{]} \tag{9} \]The impedance of the low pass filter is calculated as:
\[ Z = \sqrt{R^{2}+X_{C}^{2}} \text{ [} \Omega \text{]} \tag{10} \]When the low pass filter is applied to a sinusoidal input signal, we can also calculate the amplitude of the output voltage VOUT as:
\[ V_{OUT} = V_{IN} \cdot \frac{X_{C}}{Z} \text{ [V]} \tag{11} \]Low pass filter calculation example
Let’s calculate the parameters of a low pass filter consisting of a resistor of 5 kΩ in series with a capacitor of 20 nF connected across a 12 V sinusoidal supply. Calculate also the output voltage amplitude ( VOUT ) at a frequency of 1 Hz and again at frequency of 100 kHz.
Using the equations defined above we can calculate:
Cut-off angular frequency:
\[ \omega_{c} = \frac{1}{RC} = \frac{1}{5 \cdot 10^3 \cdot 20 \cdot 10^{-9}} = 10000 \text{ [rad/s]} \]Cut-off frequency:
\[ f_{c} = \frac{1}{2 \pi RC} = \frac{1}{2 \cdot \pi \cdot 5 \cdot 10^3 \cdot 20 \cdot 10^{-9}} = 1.5915 \text{ [kHz]} \]Period:
\[ T = 2 \pi RC = 6.2832 \cdot 10^{-4} \text{ [s]} \]Time constant:
\[ \tau = RC = 1 \cdot 10^{-4} \text{ [s]} \]Now we are going to calculate the capacitive reactance, impedance and phase shift for both input signals frequencies:
\[ X_{C} = \frac{1}{2 \pi f C} \text{ [} \Omega \text{]} \]1 Hz:
\[ X_{C} = \frac{1}{2 \cdot \pi \cdot 1 \cdot 20 \cdot 10^{-9}} = 7.9577 \cdot 10^{6} \text{ [} \Omega \text{]} \]100 kHz:
\[ X_{C} = \frac{1}{2 \cdot \pi \cdot 100 \cdot 10^{3} \cdot 20 \cdot 10^{-9}} = 79.5775 \text{ [} \Omega \text{]} \]The impedance for both input signals frequencies is:
\[ Z = \sqrt{R^{2}+X_{C}^{2}} \text{ [} \Omega \text{]} \]1 Hz:
\[ Z = \sqrt{(5 \cdot 10^{3})^{2}+(7.9577 \cdot 10^{6})^{2}} = 7.9577 \cdot 10^{6} \text{ [} \Omega \text{]} \]100 kHz:
\[ Z = \sqrt{(5 \cdot 10^{3})^{2}+(79.5775)^{2}} = 5000.6 \text{ [} \Omega \text{]} \]The phase shift is calculated as:
\[ \varphi = – \arctan \left (2 \pi f RC \right ) \text{ [rad]} \]1 Hz:
\[ \varphi = – \arctan \left (2 \cdot \pi \cdot 1 \cdot 5 \cdot 10^{3} \cdot 20 \cdot 10^(-9) \right ) = -6.2832 \cdot 10^{-4} \text{ [rad]} \]100 kHz:
\[ \varphi = – \arctan \left (2 \cdot \pi \cdot 100 \cdot 10^{3} \cdot 5 \cdot 10^{3} \cdot 20 \cdot 10^{-9} \right ) = -1.5549 \text{ [rad]} \]Having the capacitive reactance and the impedance calculated, we can calculate also the amplitude of the output voltage (filtered voltage):
\[ V_{OUT} = V_{IN} \cdot \frac{X_{C}}{Z} \text{ [V]} \]1 Hz:
\[ V_{OUT} = 12 \cdot \frac{7.9577 \cdot 10^{6}}{7.9577 \cdot 10^{6}} = 12 \text{ [V]} \]100 kHz:
\[ V_{OUT} = 12 \cdot \frac{79.5775}{5000.6} = 0.1910 \text{ [V]} \]From this exercise we can draw the following conclusions:
- the higher the input signal frequency (compared to the cut-off frequency), the higher the phase shift and the lower the amplitude
- low frequency signals pass unaltered by the RC low pass filtered, in terms of phase and amplitude
- high frequency signals have their amplitude decreased at very low levels which basically translates into being blocked (filtered)
Low pass filter mathematical analysis
The mathematical model of the low pass filter (RC circuit) can be represented in:
- Time domain (t)
- Laplace domain (s), also known as transfer function
- Discrete domain [k]
Time domain equation of the low pass filter
The time equation of the low pass filter is represented by the following differential equation:
\[v_{OUT}(t) = v_{IN}(t) – RC \cdot \frac{dv_{OUT}}{dt} \tag{12} \]Transfer function of the low pass filter
Applying the Laplace transform to the time domain differential equation (12), we get the transfer function of the low pass filter as:
\[H(s) = \frac{1}{RC \cdot s+1} \tag{13}\]The low pass filter transfer function can be written function of the cut-off angular frequency:
\[H(s) = \frac{\omega_{c}}{s + \omega_{c}} \tag{14}\]or function of the time constant:
\[H(s) = \frac{1}{\tau \cdot s + 1} \tag{15}\]Discrete equation of low pass filter
For simulation purposes of the low pass filter we can use the time domain equation or the transfer function.
If we need to use a low pass filter in an embedded application, as a software component, we’ll need a discrete version of the filter.
If we sample equation (12), with a sample time of Δt [s], the discrete model of the low pass filter will be:
\[v_{OUT}[k] = v_{IN}[k] – RC \cdot \frac{v_{OUT}[k] – v_{OUT}[k-1]}{\Delta t} \tag{16} \]where:
[k] – current calculation step
[k-1] – previous calculation step
Rearranging equation (16) gives the following discrete equation for the low pass filter:
\[v_{OUT}[k] = v_{IN}[k] \left ( \frac{\Delta t}{RC + \Delta t} \right ) + v_{OUT}[k-1] \left ( \frac{RC}{RC + \Delta t} \right ) \tag{17}\]The discrete formula of the low pass filter (17) can be written in a simplified form as:
\[v_{OUT}[k] = \alpha v_{IN}[k] + (1 – \alpha) v_{OUT}[k-1] \tag{18}\]Where α is the low pass filter smoothing factor, 0 <= α <=1:
\[\alpha = \frac{\Delta t}{RC + \Delta t} \tag{19} \]The sample time Δt is set function of the task rate at which the filter function is called. For example, if the low pass filter function is called every 10 ms, the sample time Δt must be set to 0.01 s.
Low pass filter simulation
Now that we have the mathematical models of the low pass filter we can use dedicated software for numerical analysis, like Scilab/Xcos to better understand the operation and performance of the filter.
Time domain implementation of a low pass filter into Scilab
In this example we are going to implement the time domain function of the low pass filter into Scilab and run it against different values of the resistance R and capacitance C.
// Clean figure, console and workspace variables
clf()
clc()
clear()
// Define input parameters
vIN = 12; // [V]
R_ary = [1.5 2 2.5]; // [ohm]
C_ary = [0.05 0.05 0.05]; // [F]
tau_ary = R_ary.*C_ary; // [s]
// Define t [s]
t0=0; tinc=0.001; tf=1; t=t0:tinc:tf;
// Define differential equation
function dx=f(t,x)
dx(1)=(vIN-x(1))/(R*C)
endfunction
// Define initial conditions
vC0 = 0; // [V]
// Solve differential equation
for i=1:length(R_ary)
R = R_ary(i);
C = C_ary(i);
vOUT(i,:) = ode(vC0,t0,t,f)
end
// Plot numeric solution
plot(t,vOUT(1,:),'k',"linewidth",2), xgrid
plot(t,vOUT(2,:),'r',"linewidth",2)
plot(t,vOUT(3,:),'b',"linewidth",2)
title("x-engineer.org","Color",'b',"fontsize",2)
ylabel('$\large{v_{OUT}(t) \text{ [V]}}$','fontsize',2)
xlabel('$\large{t} \text{ [s]}$','fontsize',2)
legend(strcat(['time constant = ' string(tau_ary(1)) ' s']), ..
strcat(['time constant = ' string(tau_ary(2)) ' s']), ..
strcat(['time constant = ' string(tau_ary(3)) ' s']),4)
Running the above Scilab instructions will output the following plot.
Image: Low pass filter – time constant
As you can see in the plot, the higher the time constant of the filter, the smoother the rise of the output signal.
Transfer function implementation of a low pass filter in Scilab
// Clean figure, console and workspace variables
clf()
clc()
clear()
// Define input parameters
vIN = 12; // [V]
R = 2; // [ohm]
C = 0.05; // [F]
tau = R * C; // [s]
// Define t [s]
t0=0; tinc=0.001; tf=1; t=t0:tinc:tf;
// Define transfer function
s=poly(0,'s');
Hs=[1/(R*C*s+1)];
sys=syslin('c',Hs)
// Run step response
vOUT = vIN*csim('step',t,sys);
plot(t,vOUT,"r","linewidth",2), xgrid()
hf=gcf();
hf.background = -2;
title("x-engineer.org","Color",'b','fontsize',2)
ylabel('$\large{v_{OUT}(t) \text{ [V]}}$','fontsize',2)
xlabel('$\large{t} \text{ [s]}$','fontsize',2)
Running the above Scilab instructions will output the following plot.
Image: Low pass filter – transfer function Scilab plot
Discrete model implementation of a low pass filter in Scilab
// Clean figure, console and workspace variables
clf()
clc()
clear()
// Define input parameters
vIN = 12; // [V]
R = 2; // [ohm]
C = 0.05; // [F]
Dt = 0.01; // [s]
tau = R * C; // [s]
alpha = Dt/(tau+Dt);
// Define t [s]
t0=0; tinc=0.01; tf=1; t=t0:tinc:tf;
vOUT = [];
for i=1:length(t)
if (i==1) then
vOUT(i) = 0;
else
vOUT(i) = alpha*vIN + (1-alpha)*vOUT(i-1);
end
end
plot(t,vOUT,"r","linewidth",2), xgrid()
title("x-engineer.org","Color",'b','fontsize',2)
ylabel('$\large{v_{OUT}(t) \text{ [V]}}$','fontsize',2)
xlabel('$\large{t} \text{ [s]}$','fontsize',2)
Time domain implementation of a low pass filter into Xcos
In all the Xcos block diagrams below the input of the filter (“measured” signal) is simulated as a sum of an “ideal” signal with a sinusoidal and a random noise. The purpose of the filter is to remove both the sinusoidal and random noise and output a signal (filtered) which is very close in terms of amplitude and phase with the “ideal” signal
Image: Low pass filter – differential equation – Xcos block diagram (1)
The low pass filter is implemented as the differential equation (2).
Image: Low pass filter – differential equation – Xcos block diagram (2)
After post processing the simulation results of the Xcos block diagram we can visualise the input and output signals of the low pass filter.
Image: Low pass filter – differential equation – Xcos simulation results
Transfer function implementation of a low pass filter in Xcos
Image: Low pass filter – transfer function – Xcos block diagram
After post processing the simulation results of the Xcos block diagram we can visualise the input and output signals of the low pass filter.
Image: Low pass filter – transfer function – Xcos simulation results
Discrete model implementation of a low pass filter in Xcos
Image: Low pass filter – discrete function – Xcos block diagram (1)
The low pass filter is implemented as the differential equation (18).
Image: Low pass filter – discrete function – Xcos block diagram (2)
After post processing the simulation results of the Xcos block diagram we can visualise the input and output signals of the low pass filter.
Image: Low pass filter – discrete function – Xcos simulation results
Low pass filter calculator
If you want to try out different parameters of a low pass filter and check its response to a step input or to a measured signal (simulated) use the on-line low pass filter calculator.
References
[1] Hayt, William H., Jr. and Kemmerly, Jack E. (1978). Engineering Circuit Analysis. New York: McGRAW-HILL BOOK COMPANY. pp. 211–224, 684–729.
[2] Boyce, William and DiPrima, Richard (1965). Elementary Differential Equations and Boundary Value Problems. New York: JOHN WILEY & SONS. pp. 11–24.