Bilinear interpolation

Table of Contents

• Definition
• Formula
• Example
• Scilab algorithm
• Calculator

Definition

In a previous article, Linear interpolation and extrapolation with calculator, we have discussed how linear (1-D) interpolation is done, what is the mathematical background and where it’s used. In this article we are going to follow the same principle but this time on two directions (x and y). Bilinear (2-D) interpolation is defined as linear interpolation on two directions or axes. The 1-D stand for one direction (x axis), while 2-D stands for two directions (x and y axes).

Bilinear interpolation is used in several engineering and science domain, the most common being:

• computer vision: as a basic resampling techniques and image processing (where it is also called bilinear filtering or bilinear texture mapping)
• embedded control systems: as a technique to extract values from a defined set of data.

How bilinear (2-D) interpolation works? Let’s assume that we have defined a set of data coordinates (x_k, y_k), where k = 1, 2. These coordinates define the position of the points Q₁₁, Q₂₁, Q₁₂ and Q₂₂. For any given x and y coordinates, which are located in between the x_k and y_k points, by applying bilinear interpolation technique, we can find the P point (defined by x and y).

Go back

Formula

To find point P(x, y) through biliear interpolation we need to perform the following steps:

• two linear interpolations along the x-axis, finding intermediate points R₁ and R₂
• one linear interpolation along the y-axis, finding point P

As you can see, bilinear interpolation consists of linear interpolation along both axes, two linear interpolations along x-axis and one linear interpolation along y-axis.

Point R₁(x, y) is defined as:

Point R₂(x, y) is defined as:

The interpolated point P(x, y) is defined as:

Go back

Example

For a better understanding let’s work on a practical example. Let’s assume that we have the following dataset:

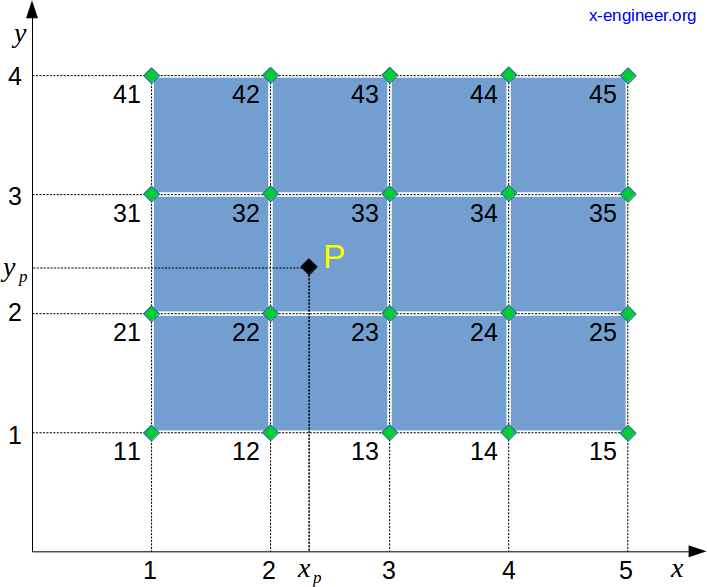
We have several data points (green diamonds), defined by a series of (x_i, y_j) coordinates, where i = 1, 2, 3, 4, 5 and j = 1, 2, 3, 4. The requirement is to find the value of point P defined by any x_p and y_p coordinates. For this example we are going to find the value of P for x_p = 2.3 and y_p = 2.4. Attention! Coordinates x_p and y_p correspond to x and y in the equations (1) , (2) and (3) above.

In an embedded control system this dataset is implemented as a map (z) with two axes (x and y). The map contains the value points and the axes contains the coordinate points. Using bilinear interpolation, for any given point x_p and y_p, we can extract the equivalent point (value) P (also known as z_p).

Step 1. Extract the Q₁₁, Q₂₁, Q₁₂ and Q₂₂ points.

As we can see from the image above, point P is situated in the rectangle defined by the values 22, 23, 32 and 33. Therefore:

Step 2. Extract the (x₁, y₁) and (x₂, y₂) coordinates.

Knowing Q-points, we can easily extract their coordinates (see image above).

Step 3. Calculate R₁ using equation (1).

Step 4. Calculate R₂ using equation (2).

Step 5. Calculate P using equation (3).

The value of P(x_p, y_p) = 26.3 (2.3, 2.4) fits the rectangle defined by the Q-points, which give us confidence on the algorithm. For further validation you can use a third party software which has a predefined 2-D interpolation function and check the result for the same input data.

Go back

Scilab algorithm

Implementing the bilinear interpolation in Scilab come with some further checks on the input data. For the algorithm to work properly, these data checks must be performed:

• check that the given input coordinates (x_p, y_p) have their value between the minimum and maximum of the axes values
• check that the x-axis has monotonically increasing values
• check that the y-axis has monotonically increasing values

The Scilab algorithm below implements the bilinear interpolation technique defined by the equation (1), (2) and (3) together with the data checks defined above. We used a *.sci file to create a custom Scilab function for the bilinear interpolation algorithm.

function [P]=f_interp2d(x, y, z, xp, yp)

    // Check if x axis is monotonically increasing
    for i=1:length(x)
        // Axis is not monotonically increasing
        if i>1 && x(i) <= x(i-1)
            //disp("Axis x is not monotonically increasing")
            break;
        end
    end

    // Find x1 and x2 coordinates
    for i=1:length(x)
        // Point xp is outside range
        if xp < x(1) || xp > x(length(x))
            //disp("Point xp is out or range");
            if xp < x(1)
                xp = x(1);
            else
                xp = x(length(x));
            end
        end

        // Point x is the first point in the axis
        if xp == x(1)
            x1 = x(1);
            x1_idx = 1;
            x2 = x(2);
            x2_idx = 2;
            break;
        end

        // Point x is the last value in the axis
        if xp == x(length(x))
            x1 = x(length(x)-1);
            x1_idx = length(x)-1;
            x2 = x(length(x));
            x2_idx = length(x);
            break;
        end

        // Point x is in between first and last point of the axis
        if xp >= x(i) && xp <= x(i+1)
            x1 = x(i);
            x1_idx = i;
            x2 = x(i+1);
            x2_idx = i+1;
            break;
        end
    end

    // Check if y axis is monotonically increasing
    for i=1:length(y)
        // Axis is not monotonically increasing
        if i>1 && y(i) <= y(i-1)
            //disp("Axis y is not monotonically increasing")
            break;
        end
    end

    // Find y1 and y2 coordinates
    for i=1:length(y)

        // Point yp is outside range
        if yp < y(1) || yp > y(length(y))
            //disp("Point yp is out or range");
            if yp < y(1)
                yp = y(1);
            else
                yp = y(length(y));
            end
        end

        // Point y is the first point in the axis
        if yp == y(1)
            y1 = y(1);
            y1_idx = 1;
            y2 = y(2);
            y2_idx = 2;
            break;
        end

        // Point y is the last value in the axis
        if yp == y(length(y))
            y1 = y(length(y)-1);
            y1_idx = length(y)-1;
            y2 = y(length(y));
            y2_idx = length(y);
            break;
        end

        // Point y is in between first and last point of the axis
        if yp >= y(i) && yp <= y(i+1)
            y1 = y(i);
            y1_idx = i;
            y2 = y(i+1);
            y2_idx = i+1;
            break;
        end
    end
    Q11 = z(y1_idx, x1_idx);
    Q12 = z(y2_idx, x1_idx);
    Q21 = z(y1_idx, x2_idx);
    Q22 = z(y2_idx, x2_idx);

    R1 = Q11*((x2-xp)/(x2-x1)) + Q21*((xp-x1)/(x2-x1));
    R2 = Q12*((x2-xp)/(x2-x1)) + Q22*((xp-x1)/(x2-x1));
    P = R1*((y2-yp)/(y2-y1)) + R2*((yp-y1)/(y2-y1)); 
    
endfunction

The Scilab instructions above are saved as the file f_interp.sci. After running the file, the function is loaded in the Scilab workspace and we can start using it. The function expects 5 parameters: x-axis, y-axis, map and the points where the interpolation is performed (x_p, y_p).

Example of usage:

x = [1;2;3;4;5];
y = [1;2;3;4];

z(4,:) = [41,42,43,44,45];
z(3,:) = [31,32,33,34,35];
z(2,:) = [21,22,23,24,25];
z(1,:) = [11,12,13,14,15];

xp = 2.3;
yp = 2.4;

P = f_interp2d(x,y,z,xp,yp)
disp(P)

Running the above instructions will return the following result in the Scilab console:

26.300000

This proves that the Scilab bilinear interpolation has been correctly implemented and we get the same result as in the previous example. This function can be also called in a incremental loop with different coordinates.

For example we want to interpolate between the minimum and maximum of each axis, with an increment of 0.1 for each axis. If we plot side by side the initial input data and the interpolated data, we’ll get the following result:

Image: Bilinear interpolation – plot of the input data

Image: Bilinear interpolation – plot of the interpolated data

Go back

Calculator

To practice your understanding of bilinear interpolation the below calculator can be used. The input data can be altered as desired within the limits imposed by data consistency (monotonic and between limits).

Attention! The map data rows are separated by “;”.

x =		x-axis size = 5
y =		y-axis size = 4
z =	11,12,13,14,15;21,22,23,24,25;31,32,33,34,35;41,42,43,44,45	map size = 4 x 5
xp =
yp =
Interpolate
R1 =
R2 =
zp =

The plot displays the input data together with the interpolated point. This way the user can easily check if the interpolated point fits the input data.