In mechanics we deal with two types of quantities (variables): scalar and vector variables. Scalar variables have only magnitude, for example: length, mass, temperature, time. Vector variables have magnitude and direction, for example: speed, force, torque. The direction of the vector is defined by the angles of the force witch each axis. The vector variables are usually represented using bold symbols with arrows on top.
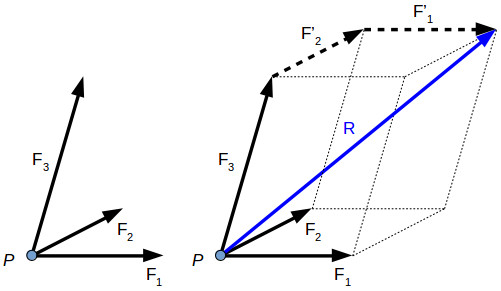
Several forces can act on a body or point, each force having different direction and magnitude. In engineering the focus is on the resultant force acting on the body. The resultant of concurrent forces (acting in the same plane) can be found using the parallelogram law, the triangle rule or the polygon rule.
Two or more forces are concurrent is their direction crosses through a common point. For example, two concurrent forces F1 and F2 are acting on the same point P. In order to find their resultant R, we can apply either the parallelogram law or triangle rule.
 | |
| Parallelogram law | Triangle rule |
The resultant force is the vector sum between the components:
\[\overrightarrow{R} = \overrightarrow{F_1} + \overrightarrow{F_2}\]If there are several forces acting on the same point, we can apply the polygon rule to find their resultant.
The resultant force can be determined also for three-dimensional force systems, by using the polygon rule.
The parallelogram law, triangle rule and polygon rule are geometric methods to find the force resultant. We can draw the force resultant but we don’t know precisely its magnitude and direction.
In order to calculate the magnitude and direction of a resultant force or to calculate the value of one force component or another, we can use the law of sines and the law of cosines.
The diagonal of the parallelogram PBCA is the resultant force R, which forms two scalene triangles with the forces F1 and F2.
Since the sum of all the angles within a triangle is 180°, we can write γ function of α and β.
\[\gamma = 180^{\circ} – \alpha – \beta \tag{1}\]The law of sines gives the relationship between the forces and the angles:
\[\frac{F_1}{\text{sin}(\alpha)} = \frac{F_2}{\text{sin}(\beta)} = \frac{R}{\text{sin}(180^{\circ} – \alpha – \beta)} \tag{2}\]The law of cosines will give us the following relationship:
\[R = \sqrt{F_1^2 + F_2^2 – 2 \cdot F_1 \cdot F_2 \cdot \text{cos}(180^{\circ} – \alpha – \beta)} \tag{3}\]The resultant force can also be calculated analytical, using force projections. Using the force projection method, we can calculate the magnitude and direction angles of the resultant force.
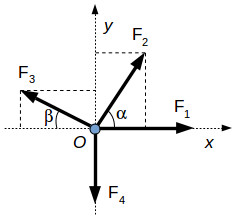
In the image above we have a resultant force R and its projections on each axis:
Fx – the projection of R on the x-axis
Fy – the projection of R on the y-axis
Fz – the projection of R on the z-axis
α – the angle between R and the x-axis
β – the angle between R and the y-axis
γ – the angle between R and the z-axis
If there are several forces acting in the same point, we’ll calculate the resultant of their projections on each axis:
\[ \begin{split}F_x &= \sum_{i=1}^{n} F_{ix}\\
F_y &= \sum_{i=1}^{n} F_{iy}\\
F_z &= \sum_{i=1}^{n} F_{iz}
\end{split} \]
where n is the number of acting forces and Fx, Fy and Fz are the force resultants on each axis.
The magnitude of the resultant force is:
\[R = \sqrt{F_x^2 + F_y^2 + F_z^2} \tag{4}\]Each axis resultant can be expressed function of the resultant R:
\[ \begin{split}F_x &= R \cdot \text{cos}(\alpha)\\
F_y &= R \cdot \text{cos}(\beta)\\
F_z &= R \cdot \text{cos}(\gamma)
\end{split} \]
Replacing (4) in the equations above gives the angles with each axis (as trigonometric functions):
\[ \begin{split}\text{cos}(\alpha) &= \frac{F_x}{\sqrt{F_x^2 + F_y^2 + F_z^2}}\\
\text{cos}(\beta) &= \frac{F_y}{\sqrt{F_x^2 + F_y^2 + F_z^2}}\\
\text{cos}(\gamma) &= \frac{F_z}{\sqrt{F_x^2 + F_y^2 + F_z^2}}
\end{split} \]
The force projection method can also be used for co-planar (x, y-axis) force resultant calculations.
Example 1. Given the forces F1 = 2.91 N, F2 = 2.67 N, F3 = 2.47 N and F4 = 2.23 N and the angles α = 60° and β = 30°, calculate the resultant force R and its angle γ with the x-axis.
Step 1. To get an idea on how the resultant force might look like, we can apply to polygon rule.
As you can see, the magnitude of the resultant is nearly equal with that of the force F3. Also, the angle γ should be around the value of α. This geometrical solution is helpful because we know what results we should expect from the analytical solution.
Step 2. Calculate the force projections on each axis.
\[ \begin{split}F_x &= F_1 + F_2 \cdot \text{cos}(\alpha) – F_3 \cdot \text{cos}(\beta) &= 2.11 \text{ N}\\
F_y &= F_2 \cdot \text{cos} \left ( \frac{\pi}{2} – \alpha \right ) + F_3 \cdot \text{cos} \left ( \frac{\pi}{2} – \beta \right ) – F_4 &= 1.32 \text{ N}
\end{split} \]
Step 3. Calculate the force resultant.
\[R = \sqrt{F_x^2 + F_y^2} = 2.48 \text{ N}\]Step 4. Calculate the angle of the force resultant with the x-axis.
\[\gamma = \text{arccos} \left( \frac{F_x}{R} \right ) \cdot \frac{180^{\circ}}{\pi} = 32^{\circ}\]As expected, the analytic solution (forces projection) give the same results as the geometric solution (polygon rule).
Example 2. Given the forces F1 = 6.12 N, F2 = 4.32 N, F3 = 1.84 N and their angles α = 16°, β = 22°, γ = 36°, calculate the force resultant R and its angles αR, βR, γR with the x, y and z axis. The forces are diagonals on each side of a rectangular parallelepiped.
Step 1. Calculate the force projections on each axis.
\[ \begin{split}F_x &= F_1 \cdot \text{cos}(\alpha) + F_2 \cdot \text{cos}(\beta) &= 9.89 \text{ N}\\
F_y &= F_1 \cdot \text{cos} \left ( \frac{\pi}{2} – \alpha \right ) + F_3 \cdot \text{cos} \left ( \frac{\pi}{2} – \gamma \right ) &= 2.77 \text{ N}\\
F_z &= F_3 \cdot \text{cos}(\gamma) + F_2 \cdot \text{cos} \left ( \frac{\pi}{2} – \beta \right ) &= 3.11 \text{ N}
\end{split} \]
Step 2. Calculate the force resultant.
\[R = \sqrt{F_x^2 + F_y^2 + F_z^2} = 10.7 \text{ N}\]Step 3. Calculate the angle of the force resultant with the x, y and z axis.
\[ \begin{split}\alpha_R &= \text{arccos} \left ( \frac{F_x}{R} \right ) \cdot \frac{180^{\circ}}{\pi} &= 22.8^{\circ} \\
\beta_R &= \text{arccos} \left ( \frac{F_y}{R} \right ) \cdot \frac{180^{\circ}}{\pi} &= 75^{\circ} \\
\gamma_R &= \text{arccos} \left ( \frac{F_z}{R} \right ) \cdot \frac{180^{\circ}}{\pi} &= 73.2^{\circ}
\end{split} \]
General approach for two-dimensional forces acting on an object
Now that we understood how to calculate the resultant force for an object, let’s take a more general approach. For two-dimensional problems, we can write down the general equations to calculate the vertical and horizontal force components as:
- horizontal component:
- vertical component:
- resultant force:
- angle of the resultant force with the horizontal axis
\arctan \left ( \frac{F_{y}}{F_{x}} \right ) \cdot \frac{180^\circ}{\pi}, \text{ if } F_{x}>0 \text{ and } F_{y}>0 \\
90^\circ + \arctan \left ( \frac{\left |F_{x} \right |}{F_{y}} \right ) \cdot \frac{180^\circ}{\pi}, \text{ if } F_{x}<0 \text{ and } F_{y}>0 \\
180^\circ + \arctan \left ( \frac{\left |F_{y} \right |}{\left |F_{x}\right |} \right ) \cdot \frac{180^\circ}{\pi}, \text{ if } F_{x}<0 \text{ and } F_{y}<0\\
270^\circ + \arctan \left ( \frac{F_{x} }{\left |F_{y}\right |} \right ) \cdot \frac{180^\circ}{\pi}, \text{ if } F_{x}<0 \text{ and } F_{y}<0\\
\end{matrix}\right.\]
Example 3. As example, let’s take the force system from Exercise 1 and calculate the resultant force and its angle with the horizontal axis (O-x).
For this method to work, all angles need to be referenced to the horizontal axis, O-x.
The forces and angles are as follows:
- F1 = 2.91 N, α1 = 0°
- F2 = 2.67 N, α2 = 60°
- F3 = 2.47 N, α3 = 150°
- F4 = 2.23 N, α4 = 270°
Step 1. Calculate the horizontal component of the resultant
\[F_{x} = 2.91 \cdot \cos (0) + 2.67 \cdot \cos (60) + 2.47 \cdot \cos (150) + 2.23 \cdot \cos (270) = 2.106 \text{ N}\]Observation: If the calculation is done on hand-held calculator of a software application, the argument of the cos() function must be given in radians, for example:
\[\cos \left ( 60 \cdot \frac{\pi}{180} \right )\]Step 2. Calculate the vertical component of the resultant
\[F_{y} = 2.91 \cdot \sin (0) + 2.67 \cdot \sin (60) + 2.47 \cdot \sin (150) + 2.23 \cdot \sin (270) = 1.32 \text{ N}\]Observation: If the calculation is done on hand-held calculator of a software application, the argument of the sin() function must be given in radians, for example:
\[\sin \left ( 60 \cdot \frac{\pi}{180} \right )\]Step 3. Calculate the resultant force
\[R = \sqrt{2.106^{2} + 1.32^{2}} = 2.48 \text{ N}\]Step 4. Calculate the resultant force angle with the horizontal axis.
\[\gamma = \text{arctan} \left ( \frac{2.106}{2.48} \right ) \cdot \frac{180}{\pi} = 32.03^{\circ}\]This method can be extended to any number of forces, as long as the force values and angles are known.
You can also check your results using the calculator below.
Force resultant calculator
| F1 [N] | F2 [N] | F3 [N] | F4 [N] | F5 [N] |
| α1 [°] | α2 [°] | α3 [°] | α4 [°] | α5 [°] |
| Horizontal force, Fx [N] = | ||||
| Vertical force, Fy [N] = | ||||
| Force angle, γ [°] = | ||||
| Resultant force, R [N] = | ||||
Use the calculator above to calculate and evaluate different distribution of forces. By hovering the mouse pointer on the line forces, you can see their coordinates which represent the Fx [N] and Fy [N] components.
Don’t forget to Like, Share and Subscribe!
Dider hossain
Find out the resultant force(R) of X,Y, Z force. Also find out the angle
of the resultant force with Y axis. The angles are as follows: a = 45
degree; b = 50 degree; c = 30 degree. pls solve the problem..
Susanne Lohmann
Hello, I would like to use two parallelogram-of-forces figures from your website for a publication. Please can you approve the use of the figures? The two figures are:
1) the figure immediately following the sentence “The resultant of concurrent forces (acting in the same plane) can be found using the parallelogram law, the triangle rule or the polygon rule.”
2) the figure on the left hand side immediately following the sentence “we can apply either the parallelogram law or triangle rule.”
Anthony Stark
Hi Susanne,
You can use the figure as long as the source is stated. If the publication is a website, a hyper link to x-engineer.org must be provided next to the figures.