5. Plant model: Vehicle
The study vehicle is considered to have Rear Wheel Drive (RWD). The vehicle model is relatively simple, defined as a mass in translation, which receives the gearbox torque (force) as traction force and the sum of road loads as resistive force.
Image: Vehicle free body diagram
The longitudinal dynamics of the vehicle is based on the following equation:
\[F_{g}=F_{w} \tag{10}\]Fg [N] – Gearbox (traction) force
Fw [N] – Wheel (resistive) force
The gearbox force is considered after the final (differential) gear, being the force which goes in the wheel hubs and propels the vehicle.
\[F_{g}= \frac{T_{g} \cdot i_{0} \cdot \eta_{0} \cdot \eta_{l}}{r_{w}} \tag{11}\]η0 [-] – final drive (differential) efficiency
ηl [-] – longitudinal (propeller) shaft efficiency
rw [m] – wheel radius
The traction force is limited to the friction force, which can be applied to the wheels.
\[F_{lim}= m_{v} \cdot g \cdot \mu_{w} \cdot c_{w} \tag{12}\]mv [kg] – vehicle mass
g [m/s2] – gravitational acceleration
μw [-] – driving wheels friction coefficient
cw [-] – driving axle load coefficient
The load coefficient shows how much weight of the vehicle is on the rear (driving) wheels. If the value is 0.65, means that 65% of the total vehicle weight is on the rear wheels.
The wheel (resistive) force is the sum of the inertial force, aerodynamic drag, rolling friction force, road slope (gradient) resistance and braking force [2].
\[F_{w} = F_{i} + F_{a} + F_{r} + F_{s} + F_{b} \tag{13}\]Fi [N] – inertia force
Fa [N] – aerodynamic force
Fr [N] – rolling resistance force
Fs [N] – road slope (gradient) force
Fb [N] – braking force
The vehicle inertia force is calculated as:
\[F_{i} = m_{v} \cdot c_{i} \cdot \frac{dv_{v}}{dt} \tag{14}\]vv [m/s] – vehicle speed
ci [-] – rotational components inertia coefficient
The inertia of the components which are rotating, for example wheels, longitudinal shaft, gears, etc., are taking into account through the coefficient ci. If this coefficient is 1.1, means that the vehicle mass is artificially increased with 10% in order to account for the inertia of the rotational components.
The aerodynamic drag force is calculated as:
\[F_{a} = \frac{1}{2} \cdot C_{d} \cdot A \cdot v_{v}^{2} \cdot \rho \tag{15}\]Cd [-] – aerodynamic drag coefficient
A [m2] – vehicle frontal area
ρ [kg/m3] – air density
The rolling resistance force is calculated as:
\[F_{r} = m_{v} \cdot g \cdot \cos(\alpha) \cdot f \tag{16}\]α [rad] – road slope angle
f [-] – rolling resistance coefficient
The road slope angle is calculated as:
\[\alpha = \arctan \left ( \frac{s}{100} \right ) \tag{17}\]s [%] – road slope (gradient)
The rolling resistance coefficient is calculated as:
\[f = C_{0} + C_{1} \cdot v_{v} + C_{2} \cdot v_{v}^{2} \tag{18}\]C0 [-] – rolling resistance constant coefficient
C1 [s/m] – rolling resistance linear coefficient
C2 [s2/m2] – rolling resistance quadratic coefficient
The road slope (gradient) force is calculated as:
\[F_{s} = m_{v} \cdot g \cdot \sin(\alpha) \tag{19}\]The braking force is modelled as a first order transfer function:
\[H(s) = \frac{K}{T \cdot s +1} = \frac{100}{0.1 \cdot s +1} \tag{20}\]K [-] – gain
T [s] – time constant
The input into the transfer function is the brake pedal position in [%]. This means that, for the brake pedal fully pressed 100 %, the braking force will be 10000 N. The time constant will filter at a small degree the pedal position coming from the Driver model.
The vehicle speed is calculated by integrating the vehicle acceleration, the result being in m/s. Further, if we integrate the speed, we can determine the offset of the vehicle, which is the distance travelled by the vehicle from the starting point.
\[x_{v} = \int v_{v} \cdot dt \tag{21}\]xv [m] – vehicle offset
We can also calculate the vehicle speed in [kph], as:
\[V_{v} = 3.6 \cdot v_{v} \tag{22}\]Vv [kph] – vehicle speed
The wheel speed in [rpm] is calculated as:
\[N_{w} = \frac{v_{v}}{r_{w}} \cdot \frac{30}{\pi} \tag{23}\]Nw [rpm] – wheel speed
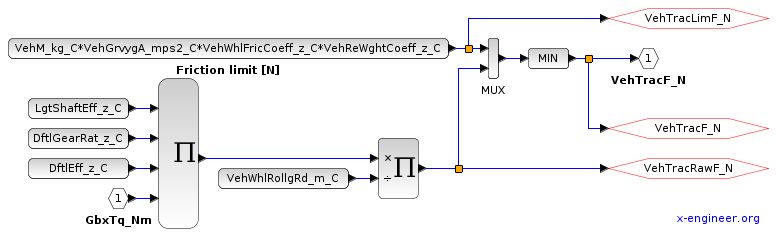
5.1 Traction force
Equations (11) and (12) are used for the Xcos model of the Traction force.
Image: Traction force – Xcos block diagram
The traction force applied at the wheel is the minimum between the raw traction for and the friction limit force.
Inputs
| Name | Value | Description |
| GbxTq_Nm | – | Gearbox torque [Nm] |
Parameters
| Name | Value | Description |
| VehM_kg_C | 2255 | Vehicle mass [kg] |
| VehGrvygA_mps2_C | 9.81 | Gravitational acceleration [m/s2] |
| VehWhlFricCoeff_z_C | 1.0 | Driving wheels friction coefficient[-] |
| VehReWghtCoeff_z_C | 0.6 | Driving axle load coefficient [-] |
| LgtShaftEff_z_C | 0.994 | Longitudinal (propeller) shaft efficiency [-] |
| DftlGearRat_z_C | 2.769 | Final gear (differential) gear ratio [-] |
| DftlEff_z_C | 0.93 | Final drive (differential) efficiency [-] |
| VehWhlRollgRd_m_C | 0.31587 | Wheel (rolling) radius [m] |
Outputs
| Name | Value | Description |
| VehTracF_N | – | Traction force (minimum between gearbox force and friction limit) [N] |
5.2 Road resistances
Equations (13), (14), (15), (16), (17), (18), (19) and (20) are used for the Xcos model of the Road resistances.
Image: Road resistance – Xcos block diagram
The road resistances can also be called as drag forces, because the oppose the movement of the vehicle.
Inputs
| Name | Value | Description |
| EnvRoadSlop_prc | – | Road slope (gradient) in [%] |
| BrkPedlPosn_prc | – | Brake pedal position in [%] |
| VehV_kph | – | Vehicle speed [kph] |
Parameters
| Name | Value | Description |
| VehM_kg_C | 2255 | Vehicle mass [kg] |
| VehGrvygA_mps2_C | 9.81 | Gravitational acceleration [m/s2] |
| VehDragCoeff_z_C | 0.29 | Aerodynamic drag coefficient [-] |
| VehFrntAr_m2_C | 2.138 | Vehicle frontal area [m2] |
| VehAirRho_kgpm3_C | 1.202 | Air density [kg/m3] |
| C0 | 1.3295·10-2 | Rolling resistance constant coefficient [-] |
| C1 | -2.8664·10-5 | Rolling resistance linear coefficient [s/m] |
| C2 | 1.8036·10-7 | Rolling resistance quadratic coefficient [s2/m2] |
Outputs
| Name | Value | Description |
| VehTotDragF_N | – | Vehicle total drag force (road resistance) [N] |
5.3 Speed calculation
Equations (10), (21), (22) and (23) are used for the Xcos model of the Speed calculation.
Image: Speed calculation – Xcos block diagram
The road resistances can also be called as drag forces, because the oppose the movement of the vehicle.
Inputs
| Name | Value | Description |
| VehTracF_N | – | Traction force (minimum between gearbox force and friction limit) [N] |
| VehTotDragF_N | – | Vehicle total drag force (road resistance) [N] |
Parameters
| Name | Value | Description |
| VehM_kg_C | 2255 | Vehicle mass [kg] |
| VehRotCmpJCoeff_z_C | 1.25 | Rotational components inertia coefficient [-] |
| VehWhlRollgRd_m_C | 0.31587 | Wheel (rolling) radius [m] |
Outputs
| Name | Value | Description |
| WhlN_rpm | – | Wheel speed [rpm] |
| VehV_kph | – | Vehicle speed [kph] |
Mirsad
Hello,
I created this model in Simulink. Everything is same with this model. When I run at full acceleration case, engine speed and turbine speed is not same as you shared. I think it is also reasonable. Because only parameter affecting engine speed is ımpeller torque and doesn’t change based on gear.
Saulnier
Hi,
Thank you for this very instructive modeling. I tried to recreate it with another car but I have different results, especially for the engine torque.
Indeed, the impeller torque become as important as the driver requested torque (the one obtained from the engine map) and I obtain a zero engine torque in output (substraction of the impeller torque from the driver requested torque in the engine plant).
Is it physically right ?
I thank you in advance for your answer,
Sincerely
A.Saulnier