3. Plant model: Engine
The engine used for the simulation example is a Mercedes 5.0 litre V8, with the following performance parameters:
- maximum engine power @ engine speed [kW@rpm]: 225 @ 5600
- maximum engine torque @ engine speed Nm@rpm]: 460 @ 3000-4250
The engine torque is mapped, function of the accelerator (throttle) position and engine speed. Only the full load data points are matched against the real engine torque output. The part load torque values are extrapolated from the full load points.
| Engine torque [Nm] | Engine speed [rpm] | |||||||||||
| 1000 | 1500 | 2000 | 2500 | 3000 | 3500 | 4000 | 4500 | 5000 | 5500 | 6000 | ||
| Accelerator pedal (throttle) position [%] | 0 | 0 | -25 | -50 | -71 | -89 | -105 | -116 | -128 | -139 | -150 | -161 |
| 20 | 241 | 155 | 93 | 57 | 30 | 6 | -16 | -36 | -53 | -68 | -81 | |
| 30 | 283 | 236 | 195 | 163 | 137 | 116 | 99 | 85 | 75 | 67 | 61 | |
| 40 | 314 | 326 | 334 | 328 | 308 | 275 | 238 | 199 | 168 | 150 | 140 | |
| 50 | 329 | 346 | 361 | 371 | 373 | 365 | 346 | 316 | 276 | 230 | 187 | |
| 60 | 349 | 365 | 378 | 387 | 396 | 398 | 384 | 357 | 322 | 284 | 246 | |
| 70 | 359 | 382 | 400 | 411 | 417 | 417 | 409 | 396 | 370 | 334 | 299 | |
| 80 | 367 | 399 | 424 | 436 | 439 | 440 | 438 | 426 | 400 | 368 | 332 | |
| 90 | 373 | 408 | 435 | 448 | 451 | 451 | 449 | 436 | 414 | 385 | 349 | |
| 100 | 377 | 414 | 443 | 456 | 460 | 460 | 460 | 450 | 427 | 402 | 366 | |
In graphical form, the engine torque output at full load and part loads looks like:
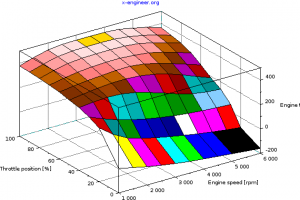 Image: Engine torque map – 3D | 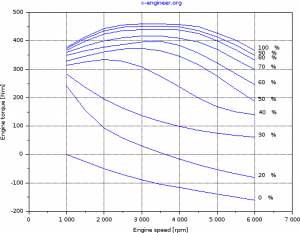 Image: Engine torque map – 2D |
The engine provides positive torque during acceleration phases and negative (braking) torque in the overrun phases. The engine is modelled as a single inertia lumped parameters and a torque map.
The governing differential equation of the engine model is:
\[J_{e} \frac{d \omega_{e} }{dt} = T_{e}-T_{i} \tag{1}\]Te [Nm] – engine torque
Ti [Nm] – impeller torque
ωe [rad/s] – engine speed
Je [kg·m2] – engine and impeller inertia
From equation (1) we can calculate the engine speed as:
\[\omega_{e} = \frac{1}{J_{e}} \int (T_{e}-T_{i}) dt \tag{2}\]To convert the engine speed from [rad/s] into [rpm], we use the following expression:
\[N_{e} = \frac{30 \cdot \omega_{e}}{\pi} \tag{3}\]Ne [rpm] – engine speed
The engine power can be calculated as:
\[P_{e} = \frac{T_{e} \cdot \omega_{e}}{1000} \tag{4}\]Pe [kW] – engine power
Equations (2), (3) and (4) are used to define the Xcos block diagram for engine simulation.
The calculated engine speed is limited to a maximum and a minimum value. The minimum value is considered the idle speed of the engine.
Inputs
| Name | Value | Description |
| ImplTq_Nm | – | Impeller torque [Nm] |
| AccrPedlPosn_prc | – | Accelerator pedal position [%] |
Parameters
| Name | Value | Description |
| EngImplJ_kgm2_C | 0.08 | Engine and impeller inertia [kg·m2] |
| EngMaxN_rpm_C | 7000 | Maximum engine speed [rpm] |
| EngMinN_rpm_C | 1000 | Minimum engine speed [rpm] |
| EngN_rpm_X | (table) | Engine speed axis [rpm] |
| AccrPedlPosnEng_prc_Y | (table) | Accelerator pedal position axis [%] |
| EngTq_Nm_Z | (table) | Engine torque map [Nm] |
Outputs
| Name | Value | Description |
| EngN_rpm | – | Engine speed [rpm] |



Mirsad
Hello,
I created this model in Simulink. Everything is same with this model. When I run at full acceleration case, engine speed and turbine speed is not same as you shared. I think it is also reasonable. Because only parameter affecting engine speed is ımpeller torque and doesn’t change based on gear.
Saulnier
Hi,
Thank you for this very instructive modeling. I tried to recreate it with another car but I have different results, especially for the engine torque.
Indeed, the impeller torque become as important as the driver requested torque (the one obtained from the engine map) and I obtain a zero engine torque in output (substraction of the impeller torque from the driver requested torque in the engine plant).
Is it physically right ?
I thank you in advance for your answer,
Sincerely
A.Saulnier