EV design – battery calculation

The high voltage battery it is one of the most important component of a battery electric vehicle (BEV). The battery parameters have a significant influence on other components and attributes of the vehicle, like:

• maximum traction motor torque
• maximum regeneration brake torque
• vehicle range
• vehicle total weight
• vehicle price

Pretty much all major aspects of a pure electric vehicle (EV) depend on the parameters of the high voltage battery.

For our electric vehicle battery design we are going to start from 4 core input parameters:

• chemistry
• voltage
• average energy consumption of the vehicle on a driving cycle
• vehicle range

A battery consists of one or more electrochemical cells (battery cells) which are converting chemical energy into electrical energy (during discharging) and electrical energy into chemical energy (during charging). The type of elements contained within a battery and the chemical reactions during discharging-charging events define the chemistry of a battery.

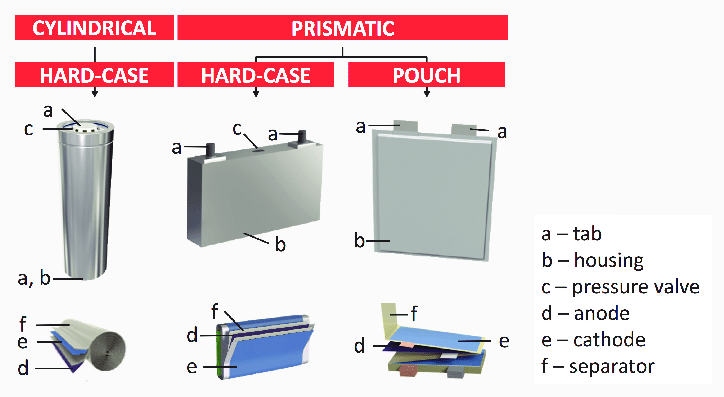
A battery cell consists of five major components: electrodes – anode and cathode, separators, terminals, electrolyte and a case or enclosure. For automotive applications there are different types of cells used [1]:

Individual battery cells are grouped together into a single mechanical and electrical unit called a battery module. The modules are electrically connected to form a battery pack.

There are several types of batteries (chemistry) used in hybrid and electric vehicle propulsion systems but we are going to consider only Lithium-ion cells. The main reason is that Li-ion batteries have higher specific energy [Wh/kg] and specific power [W/kg] compared with other types [2].

The voltage level of the battery determines the maximum electrical power which can be delivered continuously. Power P [W] is the product between voltage U [V] and current I [A]:

\[P = U \cdot I \tag{1}\]

The higher the current, the bigger the diameter of the high voltage wires and the higher the thermal losses. For this reason, the current should be limited to a maximum and the nominal power obtained by having a higher voltage. For our application we are going to consider a nominal voltage of 400 V.

In the article EV design – energy consumption we have calculated the average energy consumption for propulsion E_p as being 137.8 Wh/km on WLTC drive cycle. On top of the energy needed for propulsion, the high voltage battery must supply the energy for the vehicle’s auxiliary devices E_aux [Wh/km], like: 12 V electrical system, heating, cooling, etc. Also, we have to consider the efficiency of the powertrain η_p [-] during the conversion from electrical energy to mechanical energy.

\[E_{avg} = \left ( E_{p} + E_{aux} \right ) \cdot \left ( 2 – \eta_{p} \right ) \tag{2}\]

For the auxiliary devices energy consumption we are going to use data from [3], which contains the typical power requirements of some common vehicle electrical components (auxiliary loads). The prolonged electrical loads (headlights, multimedia, etc.) and intermittent loads (heater, brake lights, wipers, etc.) use on average 430 W of electrical power. The duration of the WLTC cycle is 1800 s (0.5 h), which gives an energy of 215 Wh for the auxiliary loads. If we divide it to the length of the WLTC driving cycle (23.266 km), we get an average energy consumption for the auxiliary loads E_aux of 9.241 Wh/km.

Even if Wh/km is not really energy but factorised energy, since it’s dived per unit of distance (km), for simplicity, we are going to refer to it as average energy.

The direct current (DC) supplied by the battery is converted into alternated current (AC) by the inverter. This conversion is taking place with an associated loss. Also, the electric motor and driveline have some losses which we need to consider. For this exercise we are going to use an average efficiency η_p of 0.9 from the battery to the wheel.

Replacing the values in (2) gives the average energy consumption:

\[E_{avg} = \left ( 137.8 + 9.241 \right ) \cdot 1.1 =  161.7451 \text{ Wh/km}\]

The battery pack will be designed for an average energy consumption of 161.7451 Wh/km.

Battery pack architectures

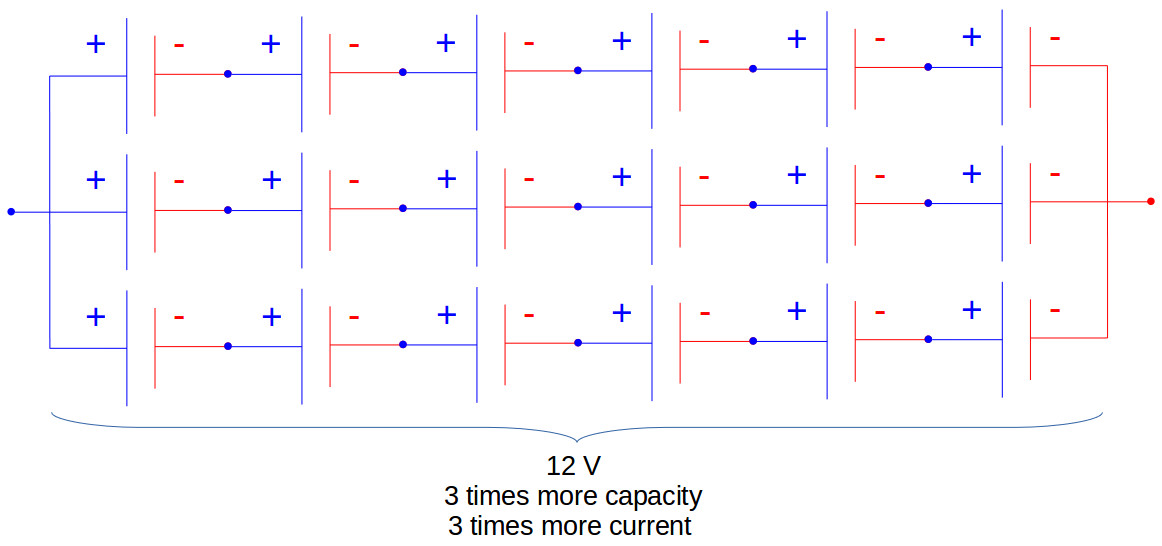
All high voltage battery packs are made up from battery cells arranged in strings and modules. A battery cell can be regarded as the smallest division of the voltage.

Individual battery cells may be grouped in parallel and / or series as modules. Further, battery modules can be connected in parallel and / or series to create a battery pack. Depending on the battery parameters, there may be several levels of modularity.

The total battery pack voltage is determined by the number of cells in series. For example, the total (string) voltage of 6 cells connected in series will be the sum of their individual voltage.

In order to increase the current capability the battery capacity, more strings have to be connected in parallel. For example, 3 strings connected in parallel will triple the capacity and current capability of the battery pack.

The high voltage battery pack of Mitsubishi i-MiEV consists of 22 modules made up from 88 cells connected in series. Each module contains 4 prismatic cells. The voltage of each cell is 3.7 V and the total voltage of the battery pack 330 V.

Another example is the high voltage battery pack of Tesla Model S, which has:

• 74 cells in a parallel group
• 6 groups in series for a module
• 16 modules in series
• 7104 cells in total

Battery pack calculation

In order to chose what battery cells our pack will have, we’ll analyse several battery cells models available on the market. For this example we are going to focus only on Lithium-ion cells. The input parameters of the battery cells are summarised in table below.

Note: Since battery cells manufacturers come up with newer models continuously, it might be the case that the data used in this example is obsolete. This is less important since the aim or the article is to explain how the calculation is done. The same method can be applied for any other battery cells.

Manufacturer	Panasonic	A123-Systems	Molicel	A123-Systems	Toshiba	Kokam
Type	cylindrical	cylindrical	cylindrical	pouch	pouch	pouch
Model	NCR18650B	ANR26650m1-B	ICR-18650K	20Ah	20Ah	SLPB7570270
Source	[4]	[5]	[6]	[7]	[8]	[9]
Length [m]	0.0653	0.065	0.0652	0	0	0
Diameter [m]	0.0185	0.026	0.0186	0	0	0
Height [m]	0	0	0	0.227	0.103	0.272
Width [m]	0	0	0	0.16	0.115	0.082
Thickness [m]	0	0	0	0.00725	0.022	0.0077
Mass [kg]	0.0485	0.076	0.05	0.496	0.51	0.317
Capacity [Ah]	3.2	2.5	2.6	19.5	20	15.6
Voltage [V]	3.6	3.3	3.7	3.3	2.3	3.6
C-rate (cont.)	1	10	1	1	1	2
C-rate (peak)	1	24	2	10	1	3

Based on the cell parameters provided by the manufacturers, we can calculate the energy content, volume, gravimetric density and volumetric density for each cell.

The volume of each cell is calculated as:

• cylindrical cells, V_cc [m³]

\[V_{cc} = \frac{\pi D_{bc}^2}{4} \cdot L_{bc} \tag{1}\]

where:
D_bc [m] – battery cell diameter
L_bc [m] – battery cell length

• pouch cells, V_pc [m³]

\[V_{pc} = H_{bc} \cdot W_{bc} \cdot T_{bc} \tag{2}\]

where:
H_bc [m] – battery cell height
W_bc [m] – battery cell width
T_bc [m] – battery cell thickness

The battery cell energy E_bc [Wh] is calculated as:

\[E_{bc} = C_{bc} \cdot U_{bc} \tag{3}\]

where:
C_bc [Ah] – battery cell capacity
U_bc [V] – battery cell voltage

The battery cell energy density is calculated as:

• volumetric energy density, u_V [Wh/m³]

\[u_{V} = \frac{E_{bc}}{V_{cc(pc)}} \tag{4}\]

• gravimetric energy density, u_G [Wh/kg]

\[u_{G} =\frac{E_{bc}}{m_{bc}} \tag{5}\]

where:
m_bc [kg] – battery cell mass

The energy density for each cells are summarised in the table below.

Manufacturer	Panasonic	A123-Systems	Molicel	A123-Systems	Toshiba	Kokam
Type	cylindrical	cylindrical	cylindrical	pouch	pouch	pouch
Model	NCR18650B	ANR26650m1-B	ICR-18650K	20Ah	20Ah	SLPB7570270
Energy [Wh]	11.52	8.25	9.62	64.35	46	56.16
Volume [l]	0.017553	0.034510	0.017716	0.263320	0.260590	0.171741
Energy density gravimetric [Wh/kg]	237.53	108.55	192.40	129.74	90.20	177.16
Energy density volumetric [Wh/l]	656.31	239.06	543.01	244.38	176.52	327

In order to have a better overview of the cells parameters and to compare them easier, the main parameters are displayed as bar graphs in the images below.

Image: Battery cell voltage	Image: Battery cell capacity
Image: Battery cell volumetric energy density	Image: Battery cell gravimetric energy density

With the above cell parameters and the core requirements for the battery (nominal voltage, average energy consumption and vehicle range), we calculate the main parameters of the high voltage battery.

The required battery pack total energy E_bp [Wh] is calculated as the product between the average energy consumption E_avg [Wh/km] and vehicle range D_v [km]. For this example we’ll design the high voltage battery pack for a vehicle range of 250 km.

\[E_{bp} = E_{avg} \cdot D_{v} = 161.7451 \cdot 250 = 40436.275 \text{ Wh} = 40.44 \text{ kWh} \tag{6}\]

The following calculations are going to be performed for each cell type. For this example we are going to consider that the battery pack is made up only from several strings connected in parallel.

The number of battery cells connected in series N_cs [-] in a string is calculated by dividing the nominal battery pack voltage U_bp [V] to the voltage of each battery cell U_bc [V]. The number of strings must be an integer. Therefore, the result of the calculation is rounded to the higher integer.

\[N_{cs} = \frac{U_{bp}}{U_{bc}} \tag{7}\]

The energy content of a string E_bs [Wh] is equal with the product between the number of battery cells connected in series N_cs [-] and the energy of a battery cell E_bc [Wh].

\[E_{bs} = N_{cs} \cdot E_{bc} \tag{8}\]

The total number of strings of the battery pack N_sb [-] is calculated by dividing the battery pack total energy E_bp [Wh] to the energy content of a string E_bs [Wh]. The number of strings must be an integer. Therefore, the result of the calculation is rounded to the higher integer.

\[N_{sb} = \frac{E_{bp}}{E_{bs}} \tag{9}\]

We can now recalculate the battery pack total energy E_bp [Wh] as the product between number of strings N_sb [-] and the energy content of each string E_bs [Wh].

\[E_{bp} = N_{sb} \cdot E_{bs} \tag{10}\]

The battery pack capacity C_bp [Ah] is calculated as the product between the number of strings N_sb [-] and the capacity of the battery cell C_bc [Ah].

\[C_{bp} = N_{sb} \cdot C_{bc} \tag{11}\]

The total number of cells of the battery pack N_cb [-] is calculated as the product between the number of strings N_sb [-] and the number of cells in a string N_cs [-].

\[N_{cb} = N_{sb} \cdot N_{cs} \tag{12}\]

The size and mass of the high voltage battery are very important parameter to consider when designing a battery electric vehicle (BEV). In this example we are going to caclulate the volume of the battery pack considering only the battery cells. In reality there are other factors to consider, like: electronic circuits, cooling circuit, battery casing, wiring, etc.

The battery pack mass (cells only) m_bp [kg] is the product between the total number of cells N_cb [-] and the mass of each battery cell m_bc [kg].

\[m_{bp} = N_{cb} \cdot m_{bc} \tag{13}\]

The volume of the battery pack (cells only) V_bp [m³] is the product between the total number of cells N_cb [-] and the mass of each battery cell V_cc(pc) [m³]. This volume is only used to estimate the final volume of the battery pack, since it does not take into account the auxiliary components/systems of the battery.

\[V_{bp} = N_{cb} \cdot V_{cc(pc)} \tag{14}\]

The volume can be also calculated function of number of strings and number of cells in a string. This calculation method is more appropriate for cylindrical cell, since the volume occupied by a cylindrical cell must take into account the air gap between cells.

The string peak current I_spc [A] is the product between the peak C-rate of the battery cell C-rate_bcp [h^-1] and the battery cell capacity C_bc [Ah].

\[I_{spc} = \text{C-rate}_{bcp} \cdot C_{bc} \tag{15}\]

The battery pack peak current I_bpp [A] is the product between the string peak current I_spc [A] and the number of strings of the battery pack N_sb [-].

\[I_{bpp} = I_{spc} \cdot N_{sb} \tag{16}\]

The battery pack peak power P_bpp [W] is the product between battery pack peak current I_bpp [A] and the battery pack voltage U_bp [V].

\[P_{bpp} = I_{bpp} \cdot U_{bp} \tag{17}\]

The string continuous current I_scc [A] is the product between the continuous C-rate of the battery cell C-rate_bcc [h^-1] and the battery cell capacity C_bc [Ah].

\[I_{scc} = \text{C-rate}_{bcc} \cdot C_{bc} \tag{18}\]

The battery pack continuous current I_bpc [A] is the product between the string continuous current I_scc [A] and the number of strings of the battery pack N_sb [-].

\[I_{bpc} = I_{scc} \cdot N_{sb} \tag{19}\]

The battery pack continuous power P_bpc [W] is the product between battery pack continuous current I_bpc [A] and the battery pack voltage U_bp [V].

\[P_{bpc} = I_{bpc} \cdot U_{bp} \tag{20}\]

The results of the equations (7) to (20) are summarised in the table below.

Manufacturer	Panasonic	A123-Systems	Molicel	A123-Systems	Toshiba	Kokam
# of cells in string [-]	112	122	109	122	174	112
String energy [Wh]	1290	1007	1049	7851	8004	6290
# of strings [-]	32	41	39	6	6	7
BP energy [kWh]	41.29	41.27	40.89	47.10	48.02	44.03
BP capacity [Ah]	102.4	102.5	101.4	117	120	109.2
# total cells [-]	3584	5002	4251	732	1044	784
BP mass [kg]*	173.8	380.2	212.6	363.1	532.4	248.5
BP volume [l]*	63	173	75	193	272	135
BP peak current [A]	102.4	2460	202.8	1170	120	327.6
BP peak power [kW]	40.96	984	81.12	468	48	131.04
BP continuous current [A]	102.4	1025	101.4	117	120	218.4
BP continuous power [kW]	40.96	410	40.56	46.8	48	87.36

BP – battery pack
* – taking into account only battery cells

From the table data we can see that the pouch type cell have better energy content and higher capacity compared with the cylindrical cells.

The same results can be plotted in bar graphs for an easier comparison between the different types of battery cells.

Image: Battery pack energy	Image: Battery pack capacity
Image: Battery pack total number of cells
Image: Battery pack mass (cells only)	Image: Battery pack volume (cells only)

Because of the low capacity for the cylindrical cells, compared to the pouch cells, the number of cells required for the battery pack is significant higher. A high number of cells might cause additional problems in areas of wiring, voltage monitoring, battery reliability.

The mass and volume are calculated only at cell level, taking into account the cell dimensions and mass. The battery pack which will be in the vehicle will have additional components (wires, electronic components, soldering, case, etc.), which will increase both the final volume and mass. Nevertheless by looking only at cell based volume and mass, we can estimate which model will be better compared to the other. In terms of mass and volume there is no clear distinction between cylindrical and pouch cells. However it seems that a battery pack with pouch cells is slightly heavier and bigger.

The battery cells manufactured by A123-Systems have very high maximum continuous discharge current and maximum pulse (peak) discharge current. As for energy and capacity, the pouch type cells have higher peak (continuous) current and power than cylindrical cells.

Based on the calculated data and conclusions, we can choose which battery cells are suitable for our electric vehicle battery pack. From our examples it looks like Kokam cells have the best compromise between mass, volume and energy/power density.

All the parameters, equations, results and plots are implemented in a Scilab (*.sce) file. For download please subscribe to the Patreon page.

You can also check your results using the calculator below.

EV Battery Calculator (on-line)

Vehicle range		Average energy consumption		Nominal battery voltage
Dv [km]		Eavg [Wh/km]		Ubp [V]
Cell type	Lbc [m]	Dbc [m]	Hbc [m]	Wbc [m]	Tbc [m]
CylindricalPouch
	mbc [kg]	Cbc [Ah]	Ubc [V]	C-ratebcc [-]	C-ratebcp [-]
Calculate
Battery Cell Performance
	Ebc [Wh]	Vbc [l]	uVbc [Wh/l]	uGbc [Wh/kg]
Battery Pack Performance
# cells / string	# strings	# cells	Es [Wh]	Ebp [kWh]	Cbp [Ah]
mbp [kg]	Vbp [l]	Ibpp [A]	Pbpp [kW]	Ibpc [A]	Pbpc [kW]

References:

[1] Mooy, Robert & Aydemir, Muhammed & Seliger, Günther. (2017). Comparatively Assessing different Shapes of Lithium-ion Battery Cells. Procedia Manufacturing. 8. 104-111. 10.1016/j.promfg.2017.02.013.
[2] Bernardini, Annalia & Barrero, Ricardo & Macharis, Cathy & Van Mierlo, Joeri. (2015). Technological solutions aiming at recovering metro braking energy: a multi-criteria analysis case study. BDC – Bollettino del Centro Calza Bini – Università degli Studi di Napoli Federico II. 14. 301-325. 10.6092/2284-4732/2929.
[3] Tom Denton, Automobile Electrical and Electronic Systems, Third edition. Elsevier Butterworth-Heinemann, 2004, page 129.
[4] https://industrial.panasonic.com/
[5] http://www.a123systems.com/
[6] http://www.molicel.com/
[7] http://www.a123systems.com/
[8] http://www.toshiba.com/
[9] http://www.kokam.com/